Question

Suppose that circles A and B have a central angle measuring 100°. Additionally, the length of the intercepted arc for circle A is 35 9 π meters and for circle B is 25 3 π meters. If the radius of circle A is 7 meters, what is the radius of circle B?

A) 9 meters
B) 12 meters
C) 15 meters
D) 18 meters

Answer 1

15 meters

253π359π = x7
x = 15

When circles have the same central angle measure, the ratio of the lengths of the intercepted arcs is the same as the ratio of the radii.

Answer 2

The correct option is C.

Explanation:

Let the radius of circle B be x.

It is given that circles A and B have a central angle measuring 100°. The length of the intercepted arc for circle A is
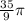`(35)/(9)\pi` meters and for circle B is
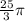`(25)/(3)\pi` meters.

The formula of length of arc is

`l=r\theta`

`\theta =(l)/(r)`

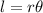
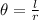
Since central angel is same for both angles, therefore

`(l_1)/(r_1)=(l_2)/(r_2)`

`((35)/(9)\pi)/(7)=((25)/(3)\pi)/(x)`

`(35)/(9* 7)\pi={(25)/(3* x)\pi`

`(5)/(9)\pi=(25)/(3x)\pi`

`x=(25)/(3)* (9)/(5)=15`

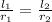
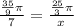
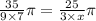
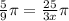
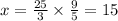
The radius of circle B is 15 meters. Therefore the option C is correct.