Answer:
The correct option is C.
Explanation:
Let the radius of circle B be x.
It is given that circles A and B have a central angle measuring 100°. The length of the intercepted arc for circle A is
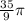 meters and for circle B is
meters and for circle B is
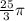 meters.
meters.
The formula of length of arc is
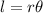
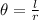
Since central angel is same for both angles, therefore
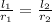
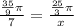

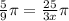
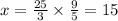
The radius of circle B is 15 meters. Therefore the option C is correct.