Answer:
B. 11
Explanation:
We have been given an image of a triangle and we are asked to find the value of n.
Since we know that in-center of a triangle is the point, where all the angle bisectors of a triangle meet.
Since we have been given that point A is the in-center of ΔDEF. This means the that DN is the angle bisector of angle EDF, so value of
 will be equal to
will be equal to
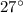
We can represent this information in an equation as:

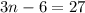


Let us divide both sides of our equation by 3.

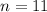
Therefore, the value of n is 11 and option B is the correct choice.