Question

(1 point) a tank contains 1060 l of pure water. a solution that contains 0.06 kg of sugar per liter enters the tank at the rate 9 l/min. the solution is mixed and drains from the tank at the same rate. (a) how much sugar is in the tank at the beginning? y(0)= 0kg (include units) (b) with s representing the amount of sugar (in kg) at time t (in minutes) write a differential equation which models this situation. s′=f(t,s)= 0.54-(9s/1060) . note: make sure you use a capital s, (and don't use s(t), it confuses the computer). don't enter units for this function. (c) find the amount of sugar (in kg) after t minutes.

Answer 1

(a) There is 0 kg of sugar in the tank at the beginning since it contains pure water at the start. The sugar only comes from the solution.

(b)


`S' = f(t,S) = \left(0.06 \frac{\text{kg}}{\text{L}}\right)\left(9\frac{\text{L}}{\text{min}}\right) - \left((S)/(1060) \frac{\text{kg}}{\text{L}}\right)\left(9\frac{\text{L}}{\text{min}}\right) \ \Rightarrow \\ \\ S' = 0.54 \text{ kg}/\text{min} - (9S)/(1060)`

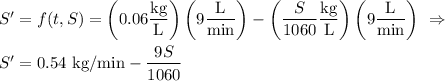
So yes, you enter S' = 0.54 - (9S/1060)

(c)


`\displaystyle(dS)/(dt) = 0.54 - (9S)/(1060) \ \Rightarrow\ (dS)/(dt) = (572.4 - 9S)/(1060)\ \Rightarrow\ (dS)/(572.4 - 9S) = (1)/(1060) dt\ \Rightarrow \\ \\ \int (dS)/(572.4 - 9S) = \int (1)/(1060) dt\ \Rightarrow\textstyle\ -(1)/(9)\ln|572.4 - 9S| = (1)/(1060)t + C \\ \\ S(0) = 0 \ \Rightarrow\ -(1)/(9)\ln|572.4 - 0| = (1)/(1060)(0) + C\ \Rightarrow\ C = -(1)/(9) \ln 572.4`


`-(1)/(9)\ln|572.4 - 9S| = (1)/(1060)t -(1)/(9) \ln 572.4\ \Rightarrow \\ \\ \ln|572.4 - 9S| = \ln 572.4 - (9)/(1060)t \ \Rightarrow \\ \\ |572.4 - 9S| = e^(\ln 572.4 - 9t/1060)\ \Rightarrow \\ \\ 572.4 - 9S= \pm 572.4 e^(-9t/1060)\ \Rightarrow \\ \\ S = (-1)/(9)\left(-572.4 \pm 572.4 e^(-9t/1060)\right)`

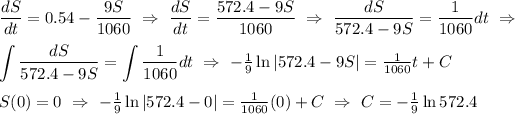
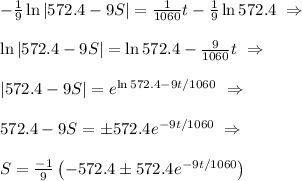
But only (+) satisfies 
`S(0) = 0`


`S= -(1)/(9)\left(-572.4 + 572.4 e^(-9t/1060)\right) \\ \\ S= 63.6 - 63.6 e^(-9t/1060)\text{ kg}`

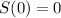
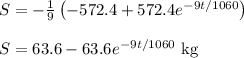
Enter in S = 63.6 - 63.6 * e^(-9t/1060)