(a) There is 0 kg of sugar in the tank at the beginning since it contains pure water at the start. The sugar only comes from the solution.
(b)

So yes, you enter S' = 0.54 - (9S/1060)
(c)

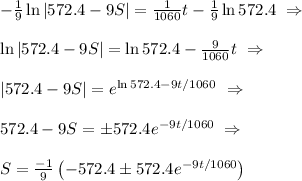
But only (+) satisfies
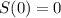
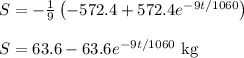
Enter in S = 63.6 - 63.6 * e^(-9t/1060)