Answer:orbital period of this GPS satellite, T= 48,874.4 s
Step-by-step explanation:
Altitude (h)= 2.25 X 10^7 m
Radius of the Earth ( r)=6.38 X 10^6 m
The distance from center of the Earth to the point is given as
R = r +h
6.38 x 10^6 m+ 2.25 x 10^7 m
=28,880,000=2.888 x 10^7m
Also, Mass of the Earth =5.97 x 10^24 kg
and Gravitational Universal Constant
= 6.67 x 10^-11N.m2/kg2
Orbital period T
= 2π
=2 X 3.142
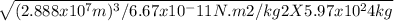
2X 3.142
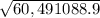
= 2X 3.142 X 7,777.60
T= 48,874.4 s