Question

A satellite is launched to orbit the Earth at an altitude of 2.25*107 m for use in the Global Positioning System (GPS). Take the mass of the Earth to be 5.97*1024 kg and its radius 6.38*106 m.

What is the orbital period of this GPS satellite?

Answer 1

Answer:orbital period of this GPS satellite, T= 48,874.4 s

Step-by-step explanation:

Altitude (h)= 2.25 X 10^7 m

Radius of the Earth ( r)=6.38 X 10^6 m

The distance from center of the Earth to the point is given as

R = r +h

6.38 x 10^6 m+ 2.25 x 10^7 m

=28,880,000=2.888 x 10^7m

Also, Mass of the Earth =5.97 x 10^24 kg

and Gravitational Universal Constant

= 6.67 x 10^-11N.m2/kg2

Orbital period T

= 2π

=2 X 3.142
`√( (2.888 x 10^7m)^3 /6.67 x 10^-11N.m2/kg2 X 5.97 x 10^24 kg)`

2X 3.142
`√(60,491088.9)`

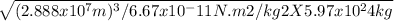
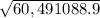
= 2X 3.142 X 7,777.60

T= 48,874.4 s