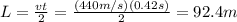Question

flipper (the dolphin) is out in the open ocean hunting tuna avec. he emits his pulse at 22khz and .42 seconds later he hears it echo bouncing back from the fat tuna (dolphins can get general ideas of size from these echoes) if these dolphin sound waves have a 2 centimeter wavelength, how far away is the tuna?

Answer 1

First we need to find the speed of the dolphin sound wave in the water. We can use the following relationship between frequency and wavelength of a wave:

`v=\lambda f`
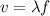
where
v is the wave speed

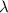
`\lambda` its wavelength
f its frequency
Using
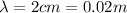
`\lambda = 2 cm = 0.02 m` and
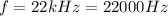
`f=22 kHz = 22000 Hz`, we get

`v=(0.02 m)(22000 Hz)=440 m/s`

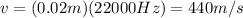
We know that the dolphin sound wave takes t=0.42 s to travel to the tuna and back to the dolphin. If we call L the distance between the tuna and the dolphin, the sound wave covers a distance of S=2 L in a time t=0.42 s, so we can write the basic relationship between space, time and velocity for a uniform motion as:

`v= (S)/(t)= (2L)/(t)`
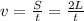
and since we know both v and t, we can find the distance L between the dolphin and the tuna:

`L= (vt)/(2)= ((440 m/s)(0.42 s))/(2)=92.4 m`