To solve this we are going to use the formula for a future value:
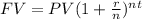
where
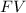
is the future value
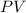
is the present value

is the interest rate in decimal form

is the number of times the interest is compounded per year
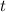
is the time in years
Since the amount needed is $42,000,
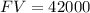
. We also know for our problem that
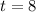
and
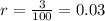
. Since the interest is compounded semiannually, it is compounded two times per year; therefore,
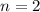
. Lets replace those values in our formula and solve for
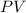
:
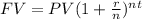
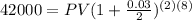
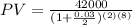
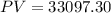
We can conclude that the present value needed to make $42000 after 8 years according to your given choices is
$33,097.26