Question

Both circle Q and circle R have a central angle measuring 75°. The ratio of circle Q's radius to circle R's radius is 2:5. Which ratio represents the area of the sector for circle R to the area of the sector for circle Q?

Answer 1

The ratio of the area of the sector for circle R to the area of the sector for circle Q is 25:4.

Explanation:

Given information: Q are R different circles. The ratio of circle Q's radius to circle R's radius is 2:5.

Let the radius of Q and R are 2x and 5x respectively.

The central angle of each circle is 75°.

The area of a sector is

`A=\pi r^2((\theta)/(360^(\circ)))`

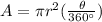
where, r is the radius of circle and θ is central angle of sector.

Area of sector of circle Q.

`A_Q=\pi (2x)^2((75^(\circ))/(360^(\circ)))`

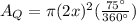
Area of sector of circle R.

`A_R=\pi (5x)^2((75^(\circ))/(360^(\circ)))`

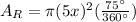
The ratio of area of sector for circle R to the area of the sector for circle Q is

`(A_R)/(A_Q)=(\pi (5x)^2((75^(\circ))/(360^(\circ))))/(\pi (2x)^2((75^(\circ))/(360^(\circ))))`

`(A_R)/(A_Q)=(25x^2)/(4x^2)`

`(A_R)/(A_Q)=(25)/(4)`

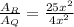
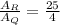
Therefore the ratio of the area of the sector for circle R to the area of the sector for circle Q is 25:4.

Answer 2

The ratio of similar areas is the square of the ratio of the scale factor.

Circle R's sector is (5/2)² = 25/4 the area of Circle Q's sector.