Answer:
The catalyzed reaction will take 2.85 seconds to occur.
Step-by-step explanation:
The activation energy of a reaction is given by:
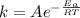
For the reaction without catalyst we have:
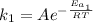 (1)
(1)
And for the reaction with the catalyst:
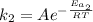 (2)
(2)
Assuming that frequency factor (A) and the temperature (T) are constant, by dividing equation (1) with equation (2) we have:

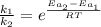

Since the reaction rate is related to the time as follow:
![k = (\Delta [R])/(t)](https://img.qammunity.org/2022/formulas/chemistry/college/bqk1cn3zt2zbg9m0kj2ncv5lvfjfeqf173.png)
And assuming that the initial concentrations ([R]) are the same, we have:
![(k_(1))/(k_(2)) = (\Delta [R]/t_(1))/(\Delta [R]/t_(2))](https://img.qammunity.org/2022/formulas/chemistry/college/uplyql68jyss5xziisk76l3vfq085tw8f4.png)
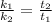
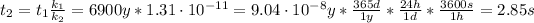
Therefore, the catalyzed reaction will take 2.85 seconds to occur.
I hope it helps you!