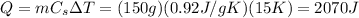Question

How much heat do you need to raise the temperature of 150 g of oxygen from -30c to -15c?

Answer 1

2.1 kJ

Step-by-step explanation:

The heat (q) required to raise the temperature of oxygen can be calculated using the following expression.

q = c × m × ΔT

where,

c: specific heat capacity (c(O₂): 0.913 J/g.°C)

m: mass

ΔT: change in the temperature

q = c × m × ΔT

q = (0.913 J/g.°C) × 150 g × [-15°C - (-30°C)] = 2.1 × 10³ J = 2.1 kJ

Answer 2

The amount of heat needed to raise the temperature of a substance by
`\Delta T` is given by

`Q=m C_s \Delta T`
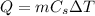
where
m is the mass of the substance
Cs is its specific heat capacity

`\Delta T` is the increase in temperature

For oxygen, the specific heat capacity is approximately

`C_s = 0.92 J/(g K)`
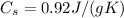
The variation of temperature for the sample in our problem is

`\Delta T= -15^(\circ)C-(-30^(\circ) C)=+15^(\circ)C=15 K`
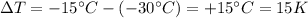
while the mass is m=150 g, so the amount of heat needed is

`Q=m C_s \Delta T=(150 g)(0.92 J/g K)(15 K)=2070 J`