Answer :
Transitive property of congruence angles.
Explanation:
Given a and b are parallel lines and c is a transversal .
To prove that

Proof:
Line
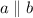 and c is a transversal line because we are given this. We can say that angles 2 and 5 are congruent by vertical opposite angle theorem because these angles are vertical opposite angles .Vertical opposite angles are those angles which are made by two intersecting lines and opposite to each other. We can say that angles 5 and 7 are congruent by corresponding angles theorem .Because angle 5 and 7 are corresponding angles .Corresponding angle are those angle which are made on the same side at each intersection where a transversal line crosses two other lines.
and c is a transversal line because we are given this. We can say that angles 2 and 5 are congruent by vertical opposite angle theorem because these angles are vertical opposite angles .Vertical opposite angles are those angles which are made by two intersecting lines and opposite to each other. We can say that angles 5 and 7 are congruent by corresponding angles theorem .Because angle 5 and 7 are corresponding angles .Corresponding angle are those angle which are made on the same side at each intersection where a transversal line crosses two other lines.
Therefore, by transitive property of congruence angles angle 2 and angle 7 are congruent.
Hence,
 .
.