Question

A company is looking to design a new cover for its smartphone. The scale drawing of the design is shown below. The coordinates of the actual cover are: R' (12, 0); S' (0, 0); T' (0, 16); U' (12, 16). Is the design of the cover similar to the actual cover?

Rectangle RSTU is shown. Point R is at 3,0. S is at 0,0. T is at 0,4. U is at 3,4.

Answer 1

yes, It is because the corresponding sides are proportional

Answer 2

Given the Vertices of Rectangle RSTU are:

R(3, 0)

S(0, 0)

T(0, 4)

U(3, 4)

Using distance formula:

`D = √((x_1-x_2)^2+(y_1-y_2)^2)`

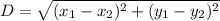
Now, the lengths of the segments be:

then;

`RS= √((3-0)^2+(0-0)^2)`

⇒
`RS = √(3^2) = 3` units

`TU= √((0-3)^2+(4-4)^2)`

⇒
`TU = √(3^2) = 3` units

`TS= √((0-0)^2+(4-0)^2)`

⇒
`TS = √(4^2) = 4` units

`UR= √((3-3)^2+(4-0)^2)`

⇒
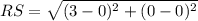
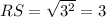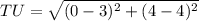
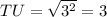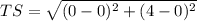
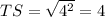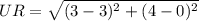
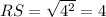`RS = √(4^2) = 4` units

It is also given:

The coordinates of the actual cover are:

R' (12, 0); S' (0, 0); T' (0, 16); U' (12, 16).

Similarly, using distance formula:

R'S' = 12 units

T'U' = 12 units

T'S' = 16 units

U'R' = 16 units

We have to find Is the design of the cover similar to the actual cover.

Two rectangles are similar if their corresponding sides are in proportional.

In Rectangle RSTU and Rectangle R'S'T'U'

`(RS)/(R'S') = (3)/(12) = (1)/(4)`

`(TU)/(T'U') = (3)/(12) = (1)/(4)`

`(TS)/(T'S') = (4)/(16) = (1)/(4)`

`(UR)/(U'R') = (4)/(16) = (1)/(4)`

⇒
`(RS)/(R'S')=(TU)/(T'U') =(TS)/(T'S')=(UR)/(U'R')`

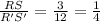
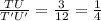
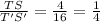
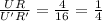
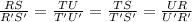
by definition;

Rectangle RSTU and Rectangle R'S'T'U' are similar

⇒Yes, because the corresponding sides are proportional.