Answer:
Given the Vertices of Rectangle RSTU are:
R(3, 0)
S(0, 0)
T(0, 4)
U(3, 4)
Using distance formula:
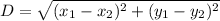
Now, the lengths of the segments be:
then;
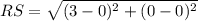
⇒
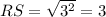 units
units
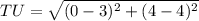
⇒
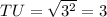 units
units
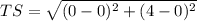
⇒
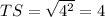 units
units

⇒
 units
units
It is also given:
The coordinates of the actual cover are:
R' (12, 0); S' (0, 0); T' (0, 16); U' (12, 16).
Similarly, using distance formula:
R'S' = 12 units
T'U' = 12 units
T'S' = 16 units
U'R' = 16 units
We have to find Is the design of the cover similar to the actual cover.
Two rectangles are similar if their corresponding sides are in proportional.
In Rectangle RSTU and Rectangle R'S'T'U'

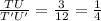
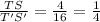

⇒
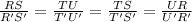
by definition;
Rectangle RSTU and Rectangle R'S'T'U' are similar
⇒Yes, because the corresponding sides are proportional.