Question

An engineer is designing a new dam for a river. The retaining wall of the dam will be angled such that the height above the ground of the top at the wall is three times the horizontal distance between where it begins and where it ends at ground level. The outer angled wall will be 100-feet long. This relationship is shown below.

Which system of equations can be used to determine y, the height above the ground at the top of the wall, and x, the horizontal distance between where the wall begins and where it ends at ground level.

Recall the Pythagorean theorem, a2 + b2 = c2, where a and b are the side lengths of a right triangle, and c is the length of the hypotenuse.

Answer 1

A system of equations that can be used to determine the height (y) above the ground at the top of the wall and the horizontal distance (x) between where the wall begins and where it ends at ground level is:

A.
`\left\{\begin{array}{Ir}x^2+y^2=100^2 \\y=3x \end{array}\right`

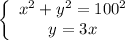
In Mathematics and Geometry, Pythagorean's theorem is an Euclidean postulate that can be modeled or represented by the following mathematical equation:

`c^2=a^2+b^2`

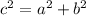
Where:

• a is the opposite side of a right-angled triangle.
• b is the adjacent side of a right-angled triangle.
• c is the hypotenuse of a right-angled triangle.

By applying Pythagorean's theorem, the right-angled triangle can be modeled by this equation;

`x^2+y^2=100^2`

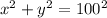
Since the retaining wall of the dam was angled to make the height (y) above the ground of the top at the wall to be three times the horizontal distance (x) between where it begins and where it ends at ground level, we have;

y = 3x

Answer 2

By the Pythagorean theorem we have:
x ^ 2 + y ^ 2 = 100 ^ 2
Then, we have:
"the height above the ground of the top at the wall is three times the horizontal distance between where it begins and where it ends at the ground level"
y = 3x
Answer:
The system of equations is:
x ^ 2 + y ^ 2 = 100 ^ 2
y = 3x