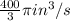Question

The radius of a right circular cone is increasing at a rate of 2 inches per second and its height is decreasing at a rate of 4 inches per second. At what rate is the volume of the cone changing when the radius is 10 inches and the height is 20 inches

Answer 1

The volume of cone changing at rate
`(400)/(3)\pi in^3/s`

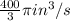
Explanation:

Let r be the radius of cone and h be the height of cone

`(dr)/(dt)=2 in/s`

`(dh)/(dt)=-4 in/s`

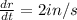
We have to find the rate at which the volume of cone changing when r=10 in and h=20 in

Volume of cone

`V=(1)/(3)\pi r^2 h`

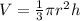
Differentiate w.r.t t

`(dV)/(dt)=(1)/(3)\pi (2rh(dr)/(dt)+r^2(dh)/(dt))`

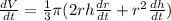
Substitute the values

`(dV)/(dt)=(1)/(3)\pi(2* 10* 20* 2+(10)^2* (-4))`

`(dV)/(dt)=(1)/(3)\pi(400)=(400)/(3)\pi in^3/s`

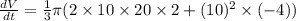
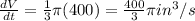
Hence, the volume of cone changing at rate
`(400)/(3)\pi in^3/s`