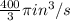Answer:
The volume of cone changing at rate
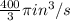
Explanation:
Let r be the radius of cone and h be the height of cone
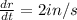
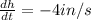
We have to find the rate at which the volume of cone changing when r=10 in and h=20 in
Volume of cone
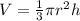
Differentiate w.r.t t
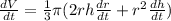
Substitute the values
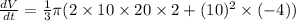
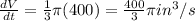
Hence, the volume of cone changing at rate