Question

Pls help I’m really confused


Find AB round to the nearest tenth if necessary

Answer 1

`AB=12.12`

Explanation:

Using intersecting secant theorem that is:

If two secant segments are drawn to a circle from an exterior point, then the product of the measures of one secant segment and its external secant segment is equal to the product of the measures of the other secant segment and its external secant segment.]

Thus,
`AB{*}AC=(AD)^2`

`AB{*}(AB+BC)=(AD)^2`

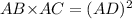
Substituting the given values, we get

`AB(AB+9)=256`

`(AB)^2+9AB=256`

`(AB)^2+9AB-256=0`

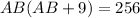
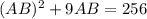
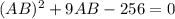
using the quadratic formula, we have

`AB=\frac{-9{\pm}√((9)^2-4(1)(-256))}{2}`

`AB=\frac{-9{\pm}√(81+1024)}{2}`

`AB=\frac{-9{\pm}√(1105)}{2}`

`AB=\frac{-9{\pm}33.24}{2}`

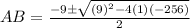
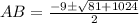
Then,
`AB=12.12` and
`AB=-21.12`

Since, AB cannot be negative, thus the measure of AB is 12.1.

Answer 2

Comment
By similar triangles it can be shown that AD^2 = AB*AC
If you want the proof, Google tangents and secants of a circle.

Find
So we want
AB

Givens
AD = 16
BC = 9

AB = ??
CA = CB + AB
CA = 9 + AB

Formula
AB * (AB + BC) = AD^2

Sub and Solve
AB*(AB + 9) = 16^2
AB*(AB + 9) = 256 Remove the brackets.
AB^2 + 9AB = 256 Subtract 256 from both sides.
AB^2 + 9AB - 256 = 0

You can only do this either with a graph or the quadratic formula. I'll get the graph for you. You can made these yourself at Desmos.

x = [-b +/- sqrt(b^2 - 4ac)] / (2a)
a = 1
b = 9
c = -256

Answer
When you substitute these into the quadratic formula, you get
x1 = 12.12 and
x2 = -21.12
x2 is meaningless. The solution is
x = 12.12

Comment
But that's not your question. Your question is what is this rounded to the nearest 1/10th? That's a fancy way of saying round to the first decimal place. Since the hundredth place (or second place) is 2, 12.12 rounds to 12.1

The answer is
x = 12.1 <<<<< answer.