Answer:
a)
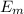 = 133.75 Gpa
= 133.75 Gpa
b) Fnet = 560 N
c) thermal expansion of the composite material = 14.31
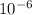 / °C
/ °C
Step-by-step explanation:
Solution:
a) Elastic Modulus of the composite:
Area of steel wire =
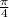 x (
x (
 ) = 0.8 x
) = 0.8 x
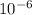

Area of Copper wire =
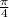 x (
x (
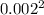 ) - 0.8 x
) - 0.8 x
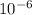

Area of Copper wire = 2.4 x
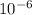

Young's Modulus of Composite mixture:
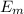 =
=
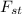
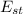 +
+

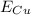 Equation 1
Equation 1
here,
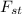 = Stress in Steel
= Stress in Steel
 = Stress in Copper.
= Stress in Copper.
We know that,
F = P/A
F is inversely proportional to Area, so if area is large, stress will less and vice versa. So, Take
Ratio for area of steel =
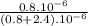
Ratio for area of steel =
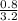 = 0.25
= 0.25
Similarly, for Copper,
Ratio for area of copper =
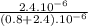
Ratio for area of copper =
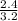 = 0.75
= 0.75
Put these values in equation 1:
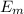 =
=
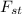
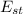 +
+

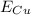
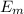 = (0.25)
= (0.25)
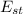 + (0.75)
+ (0.75)
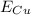
We are given that,
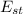 = 205 Gpa
= 205 Gpa
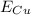 = 110 Gpa
= 110 Gpa
So,
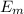 = (0.25) (205 Gpa) + (0.75) (110 GPa)
= (0.25) (205 Gpa) + (0.75) (110 GPa)
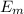 = 51.25GPa + 82.5 Gpa
= 51.25GPa + 82.5 Gpa
Hence, the Elastic Modulus of the composite will be:
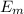 = 133.75 Gpa
= 133.75 Gpa
b) maximum force:
Fnet = Fst + Fcu
We know that F = (Yield Stress x Area)
F = fst x Ast + fcu x Acu
And we are given that,
Yield stress of Steel = 280 Mpa
Yield stress of Copper = 140 Mpa
And,
Ast = 0.8 x

Acu = 2.4 x

Just plugging in the values, we get:
F = (280 Mpa) (0.8 x
 ) + (140 Mpa) (2.4 x
) + (140 Mpa) (2.4 x
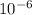
 )
)
F = 224 + 336
Fnet = 560 N ( because Mpa =
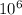 N/
N/
 )
)
So, it means the composite will carry the maximum force of 560N
c) Coefficient of Thermal Expansion:
Strain on both material is same upon loading so,
(ΔL/L)st = (ΔL/L)cu
by thermal expansion equation:
(
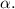 ΔT +
ΔT +
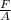
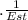 ) =
) =
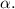 ΔT +
ΔT +
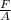
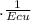 )
)
Where
 = Coefficient of Thermal expansion
= Coefficient of Thermal expansion
Here, fst = -fcu = F
and ΔT = 1°
So,
Plugging in the values, we get.
( 10 x
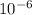 x (1) +
x (1) +
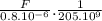 ) = ( 17 x
) = ( 17 x
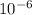 x (1) +
x (1) +
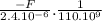 )
)
Solving for F, we get:
F = 0.71 N
Here,
fst = F = 0.71 N (Tension on Heating)
fcu = -F = 0.71 N ( Compression on Heating )
So, the combined thermal expansion of the composite material will be:
(ΔL/L)cu = ( 17 x
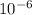 x (1°) +
x (1°) +
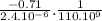 )
)
(ΔL/L)cu = ( 17 x
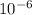 x (1°) - 2.69 x
x (1°) - 2.69 x
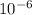
combined thermal expansion of the composite material = 14.31
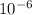 / °C
/ °C