Answer:
The correct option is 1. The function f(x) has the largest maximum.
Explanation:
The vertex form of a parabola is
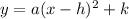
Where, (h,k) is vertex.
The given functions is
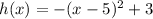
Here, a=-1, h=-5 and k=3. Since the value of a is negative, therefore it is an downward parabola and vertex is the point of maxima.
Thus the maximum value of the function h(x) is 3.
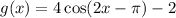
The value of cosine function lies between -1 to 1.
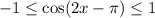
Multiply 4 on each side.
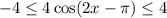
Subtract 2 from each side.
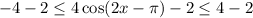
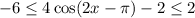
Therefore the maximum value of the function g(x) is 2.
From the given table it is clear that the maximum value of the function f(x) is 4 at x=3.
Since the function f(x) has the largest maximum, therefore the correct option is 1.