Question

A loan is amortized over five years with monthly payments (i.e. end of month) at an annual nominal interest rate of 5% compounded monthly. the first payment is 500 and is to be paid one month from the date of the loan. each succeeding monthly payment will be 20 more than the prior payment. calculate the outstanding loan balance immediately after the 40th payment is made.

Answer 1

Given:
Amortizing period = 5 years
APR=5% per annum
interest rate, i = 0.05/12 per month
number of periods, n = 5*12=60 months (for amortization)
Payment schedule:
$500 at the end of first month,
increased by $20 each month thereafter.
Borrowed amount: not given

Question: Find outstanding loan balance after the 40th payment.

Solution:
Step 1: First we need to find the amount borrowed, P.
From the payment schedule, we decompose the payment into two components,

A. Equivalent uniform monthly payment, As, for a step amount of G=$20 a month, starting with zero after the first month, for a period of 5 years (n=60).
The value of As can be obtained from a specialized formula for step-payments,

`As=(G((1+i)^(n)-i*n-1))/(i(1+i)^(n)-i)`
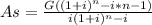
Substitute values, G=20,i=0.05/12,n=60

`As=(20((1+.05/12)^(60)-(.05/12)*60-1))/((.05/12)(1+.05/12)^(60)-(.05/60))`
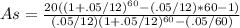
=565.0847

B. Principal, Pb, for a uniform monthly payment of A a month
The principal,Pb can be found from the basic amortizing formula to be

`Pb=(A((1+i)^(n)-1))/(i(1+i)^(n))`
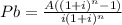
We have
Equivalent uniform monthly payment
=500+equivalent uniform payment step amounts
=500+565.0847
=1065.0847
substituting values, A=1065.0847,i=.05/12,n=60

`=(1065.0847((1+.05/12)^(60)-1))/((.05/12)(1+.05/12)^(60))`
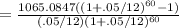
=56439.591
check: average monthly payment = 1100
duration: 60 months
total amount paid = 60*1100=66000
average annual interest=((66000-56439)/56439-1)/5=3.3% (~ 5%/2) ok.

Amount borrowed, P=56439.591

Step 2: Future value of loan at the end of the 40th month.
This can be found by the compound interest formula
F=P(1+i)^n=56439.591(1+0.05/12)^40=66652.416

Step 3: Future value of payments
first we need to find the equivalent monthly payment of the step payments, using the same formula as in step 1, but with n=40

`A=(G((1+i)^(n)-i*n-1))/(i(1+i)^(n)-i)`

`=(20((1+0.05/12)^(40)-(0.05/12)*40-1))/((0.05/12)(1+0.05/12)^(40)-(0.05/12))`
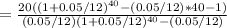
=378.924
This should be added to the constant payment of $500 a month to give
A=500+378.924=878.924
Future value of monthly payment of 878.924

`F=(A((1+i)^(n)-1))/(i)`
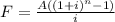
Substitute values, A=878.924, i=0.05/12, n=40

`=(878.924((1+0.05/12)^(40)-1))/(0.05/12)`
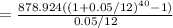
=38170.213

Step 4: Outstanding balance right after the 40th payment
=future value of loan - future value of payments
=66652.416-38170.213
=28482.20

Answer: Outstanding balance after the 40th payment is $28482.20