Given:Amortizing period = 5 years
APR=5% per annum
interest rate, i = 0.05/12 per month
number of periods, n = 5*12=60 months (for amortization)
Payment schedule:
$500 at the end of first month,
increased by $20 each month thereafter.
Borrowed amount: not given
Question: Find outstanding loan balance after the 40th payment.Solution:Step 1: First we need to find the amount borrowed, P.
From the payment schedule, we decompose the payment into two components,
A. Equivalent uniform monthly payment, As, for a step amount of G=$20 a month, starting with zero after the first month, for a period of 5 years (n=60).
The value of As can be obtained from a specialized formula for step-payments,
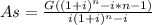
Substitute values, G=20,i=0.05/12,n=60
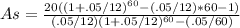
=565.0847
B. Principal, Pb, for a uniform monthly payment of A a month
The principal,Pb can be found from the basic amortizing formula to be
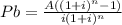
We have
Equivalent uniform monthly payment
=500+equivalent uniform payment step amounts
=500+565.0847
=1065.0847
substituting values, A=1065.0847,i=.05/12,n=60
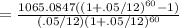
=56439.591
check: average monthly payment = 1100
duration: 60 months
total amount paid = 60*1100=66000
average annual interest=((66000-56439)/56439-1)/5=3.3% (~ 5%/2) ok.
Amount borrowed,
P=56439.591Step 2: Future value of loan at the end of the 40th month.
This can be found by the compound interest formula
F=P(1+i)^n=56439.591(1+0.05/12)^40=
66652.416Step 3: Future value of payments
first we need to find the equivalent monthly payment of the step payments, using the same formula as in step 1, but with n=40
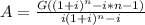
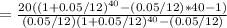
=378.924
This should be added to the constant payment of $500 a month to give
A=500+378.924=878.924
Future value of monthly payment of 878.924
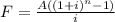
Substitute values, A=878.924, i=0.05/12, n=40
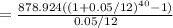
=
38170.213Step 4: Outstanding balance right after the 40th payment
=future value of loan - future value of payments
=
66652.416-38170.213
=
28482.20Answer: Outstanding balance after the 40th payment is $
28482.20