You are told that ΔABC ~ ΔDEC, which means that they are similar triangles. The ratio of similar sides of similar triangles will be the same. This means that the ratio of
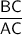
should be equal to the ratio of
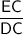
. BC is equal to 20 + 10 = 30, AC is equal to 'x + 6', EC is equal to 20, and DC is equal to 'x', let's plug these in and solve for 'x':
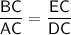
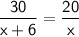
Cross multiply:
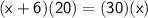
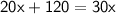
Subtract 20x to both sides:
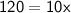
Divide 10 to both sides:
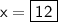
So DC is 12 units long.