Question

ΔABC​ ~ ΔDEC. ∠1 and ∠2 have the same measure. Find DC and. DE (Hint: Let DC = x and AC =x+66.)

Use the figure shown.

DC is ___ ​unit(s) long.

​(Round to the nearest tenth as​ needed.)

Answer 1

x : 20 = x+6 : 30
30x = 20x + 120
10x = 120
x = 12

DC is 12 units long

Answer 2

You are told that ΔABC​ ~ ΔDEC, which means that they are similar triangles. The ratio of similar sides of similar triangles will be the same. This means that the ratio of
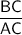
`\sf(BC)/(AC)` should be equal to the ratio of
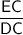
`\sf(EC)/(DC)`. BC is equal to 20 + 10 = 30, AC is equal to 'x + 6', EC is equal to 20, and DC is equal to 'x', let's plug these in and solve for 'x':


`\sf(BC)/(AC)=(EC)/(DC)`


`\sf(30)/(x+6)=(20)/(x)`

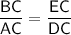
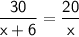
Cross multiply:


`\sf (x+6)(20)=(30)(x)`


`\sf 20x+120=30x`

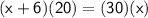
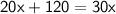
Subtract 20x to both sides:


`\sf 120=10x`

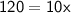
Divide 10 to both sides:


`\sf x=\boxed{\sf 12}`

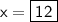
So DC is 12 units long.