Solution:
we have been asked to write the given function in vertex form

As we know that the vertex form is

So Re-write the P(x) in the above form
![p(x) =-8x^2-64x\\ \\ P(x)=-8[x^2+8]\\ \\ P(x)=-8[x^2+2.x.4+4^2-4^2]\\ \\ p(x)=-8[(x+4)^2-16]\\ \\ P(x)=-8(x+4)^2+128\\](https://img.qammunity.org/2019/formulas/mathematics/high-school/v4e5svuerzqb7l1me7ansihyu3mzrh4i6y.png)
So we have
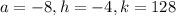
vertically stretch the graph by a factor of 8
Shift the parent function Up by 128 units.
Shift parent function left by 4 units.