Question

The function p(x) = –8x2 – 64x can be written in vertex form p(x) = a(x – h)2 + k, where a =, h =, and k =. To graph the function p, reflect the graph of f(x) = x2 across the x-axis, vertically stretch the graph by a factor of 8, shift the graph units, and then shift the graph units.

Answer 1

a= -8

h= -4

k= 128

Shift the graph left 4 units.

Then shift the graph up 128 units.

Answer 2

we have been asked to write the given function in vertex form

`p(x) =-8x^2-64x`

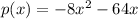
As we know that the vertex form is

`p(x) = a(x-h)^2 + k`

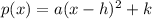
So Re-write the P(x) in the above form

`p(x) =-8x^2-64x\\ \\ P(x)=-8[x^2+8]\\ \\ P(x)=-8[x^2+2.x.4+4^2-4^2]\\ \\ p(x)=-8[(x+4)^2-16]\\ \\ P(x)=-8(x+4)^2+128\\`

So we have
`a=-8, h=-4, k=128`

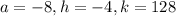
vertically stretch the graph by a factor of 8

Shift the parent function Up by 128 units.

Shift parent function left by 4 units.