Answer:
The correct option is 2.
Explanation:
The given inequality is
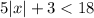
Subtract 3 from both the sides.
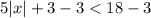
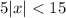
Divide both sides by 5.
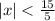
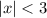
If |x|<a, then the solution set is -a<x<a.
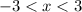
-3 and 3 are not included in the solution set because the sign of inequality is <. So, there are open circle at x=3 and x=-3.
Only graph 2 represents the solution set.
Therefore the correct option is 2.