Question

Plz answer it........

Answer 1

Okay,
so,
The given expression is :

`16{(a + b)}^(2) - 49 {(a - b)}^(2)`

As 16 is sqaure of 4 and 49 is square of 7, then this whole expression could also be written as


`{{((4)(a + b))}}^(2) - {{((7)(a - b))}}^(2)`
Now,
as you might've notices by now that this expression is in the form of


`{x}^(2) - {y}^(2)`
And there's an alzebric identity about it. That is

`{x}^(2) - {y}^(2) = (x + y)(x - y)`
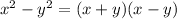
Now by using this alzebric identity. we're gonna split our expession as shown below:

`(4(a + b) + 7(a - b)) * (4(a + b) - 7(a - b) \\ \\ = (4a + 4b + 7a - 7b) * (4a + 4b - 7a + 7b) \\ = (11a - 3b)( 11b - 3a)`




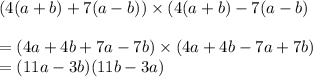
By solving the last step i.e,
(11a-3b)(11b-3a)

we'll get,
121a^2 - 33ab -33b^2 -8ab

= 121a^2-33b^2 -41ab .