Answer:
The simplified form of the expression is
![\sqrt[3]{2x}-6\sqrt[3]{x}](https://img.qammunity.org/2019/formulas/mathematics/college/rvk9h4tkf3hfu5fxwpmjex2tzi1w4q9941.png)
Explanation:
Given : Expression
![7\sqrt[3]{2x}-3\sqrt[3]{16x}-3\sqrt[3]{8x}](https://img.qammunity.org/2019/formulas/mathematics/college/t9hqqwatweh4nunwpgkplzioo1pubyc1h0.png)
To Simplified : The expression
Solution :
Step 1 - Write the expression
![7\sqrt[3]{2x}-3\sqrt[3]{16x}-3\sqrt[3]{8x}](https://img.qammunity.org/2019/formulas/mathematics/college/t9hqqwatweh4nunwpgkplzioo1pubyc1h0.png)
Step 2- Simplify the roots and re-write as
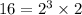 and
and
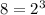
![7\sqrt[3]{2x}-3*2\sqrt[3]{2x}-3*2\sqrt[3]{x}](https://img.qammunity.org/2019/formulas/mathematics/college/ih0sbm2h86bcadf1wlfhcplv7txqx15lz5.png)
Step 3- Solve the multiplication
![7\sqrt[3]{2x}-6\sqrt[3]{2x}-6\sqrt[3]{x}](https://img.qammunity.org/2019/formulas/mathematics/college/78oo8fiyk3ucktqvkgucxkf73jrly1nbs9.png)
Step 4- Taking
![\sqrt[3]{2x}](https://img.qammunity.org/2019/formulas/mathematics/college/zoxt68bkz7rsqaw0vkt9welse65bbm59ph.png) common from first two terms
common from first two terms
![\sqrt[3]{2x}(7-6)-6\sqrt[3]{x}](https://img.qammunity.org/2019/formulas/mathematics/college/6aoj5cd2bc6w0u98ucdfg4ni9i8575iein.png)
![\sqrt[3]{2x}-6\sqrt[3]{x}](https://img.qammunity.org/2019/formulas/mathematics/college/rvk9h4tkf3hfu5fxwpmjex2tzi1w4q9941.png)
Therefore, The simplified form of the expression is
![\sqrt[3]{2x}-6\sqrt[3]{x}](https://img.qammunity.org/2019/formulas/mathematics/college/rvk9h4tkf3hfu5fxwpmjex2tzi1w4q9941.png)