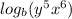Answer:
The given expression
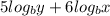 can be written as a single logarithm as
can be written as a single logarithm as
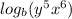
Explanation:
Consider the given expression,
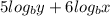
Using the property of logarithm,
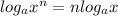
Applying reverse of above property, given expression becomes,
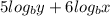
 ...(1)
...(1)
Now again using the property of logarithm
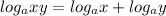
(1) can be written as,
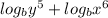
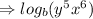
Thus, the given expression
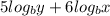 can be written as a single logarithm as
can be written as a single logarithm as