Answer:
4.21 standard deviation below mean.
Explanation:
We have been given that the average electricity bill for Lynn’s home is $64.50 per month with a standard deviation of $8.20. In June she received a bill of only $30.00.
We will use z-score formula to solve our given problem.
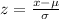 , where,
, where,
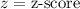 ,
,
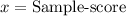 ,
,
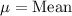 ,
,

Upon substituting our given values in z-score formula we will get,
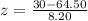

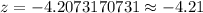
Since z-score is negative, therefore, the amount of Lynn’s electricity bill for June is approximately 4.21 standard deviations below mean.