Question

find the total pressure of a gas that initially occupied 27 L at 32 degrees Celsius and 2.5 atm, if the final conditions are 12 degrees celsius and 88.0 L

Answer 1

ideal gas law P1*V1/T1 = P2*V2/T2

so P2= P1*V1/T1 * T2/V2

P1: 2.5, V1: 27L, T1: 32C=305K

P2: ? , V2: 88L, T2: 12C=285K

P2= 2.5*27/305 * 285/88

= 0.72 atm

Answer 2

Answer: Total pressure of the gas will be 0.716atm.

Step-by-step explanation: We are given a gas having initial conditions as

V = 27L

T = 32°C = 305K

P = 2.5atm

As the gas remains same, number of moles of a gas will also be same for initial and final conditions. To calculate the number of moles, we use ideal gas equation, which is,

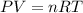`PV=nRT` .......(1)

where, R = gas constant =
`\text{0.08206 L atm }mol^(-1) K^(-1)`

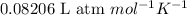
For calculating number of moles:

`n=(PV)/(RT)`

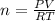
Putting the values of initial condition in this equation, we get

`n=\frac{(2.5atm)(27L)}{\text{(0.08206 L atm }mol^(-1) K^(-1))(305K)}`

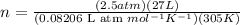
n = 2.696 mol

Now, the final conditions are,

V = 88.0L

T = 12°C = 285K

n = 2.696 mol (calculated above)

P = ? atm

Again using equation 1, we get

`P=(nRT)/(V)`

`P=\frac{(2.696mol)(\text{0.08206 L atm }mol^(-1) K^(-1))(285K)}{88.0L}`

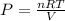
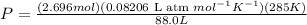
P = 0.716atm.