Answer: Total pressure of the gas will be 0.716atm.
Step-by-step explanation: We are given a gas having initial conditions as
V = 27L
T = 32°C = 305K
P = 2.5atm
As the gas remains same, number of moles of a gas will also be same for initial and final conditions. To calculate the number of moles, we use ideal gas equation, which is,
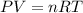 .......(1)
.......(1)
where, R = gas constant =
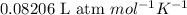
For calculating number of moles:
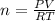
Putting the values of initial condition in this equation, we get
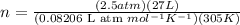
n = 2.696 mol
Now, the final conditions are,
V = 88.0L
T = 12°C = 285K
n = 2.696 mol (calculated above)
P = ? atm
Again using equation 1, we get
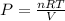
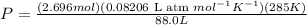
P = 0.716atm.