Answer:
![f^(-1)(x)=\sqrt[3]{(1)/(7)(x-2)}](https://img.qammunity.org/2019/formulas/mathematics/high-school/22qh4f232qw3unyv8i8sco4877i0woityt.png)
Explanation:
The given equation is
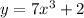
For finding inverse of this function, we apply below steps:-
Step 1
Interchange x and y
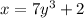
Step 2
Solve the equation for y
For this, subtract 2 to both sides of the equation
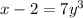
Divide both sides by 7
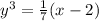
Take cube root both sides,
![y=\sqrt[3]{(1)/(7)(x-2)}](https://img.qammunity.org/2019/formulas/mathematics/high-school/fhd57xcwm5zqm253g26a3f4i5mmf9atktt.png)
Step 3
Replace y with
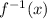
Therefore, the inverse function is
![f^(-1)(x)=\sqrt[3]{(1)/(7)(x-2)}](https://img.qammunity.org/2019/formulas/mathematics/high-school/22qh4f232qw3unyv8i8sco4877i0woityt.png)