Question

Determine the equation of the inverse of y=7x^(3)+2

Answer 1

the inverse of the equation would be solving for x, so the answer is..
the square root of y-2 with 3 as the index, and the whole equation divided by 7 the equaled to x.


`\sqrt[3]{y-2}/7 = X`

Answer 2

`f^(-1)(x)=\sqrt[3]{(1)/(7)(x-2)}`

Explanation:

The given equation is
`y=7x^3+2`

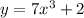
For finding inverse of this function, we apply below steps:-

Step 1

Interchange x and y

`x=7y^3+2`

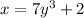
Step 2

Solve the equation for y

For this, subtract 2 to both sides of the equation

`x-2=7y^3`

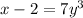
Divide both sides by 7

`y^3=(1)/(7)(x-2)`

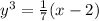
Take cube root both sides,

`y=\sqrt[3]{(1)/(7)(x-2)}`

Step 3

Replace y with
`f^(-1)(x)`

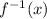
Therefore, the inverse function is

`f^(-1)(x)=\sqrt[3]{(1)/(7)(x-2)}`