Question

Chocolate chip cookies have a distribution that is approximately normal with a mean of 24.1 chocolate chips per cookie and a standard deviation of 2.1 chocolate chips per cookie. find upper p 5 and upper p 95. how might those values be helpful to the producer of the chocolate chip​ cookies?

Answer 1

Explanation:

Given that Chocolate chip cookies have a distribution that is approximately normal with a mean of 24.1 chocolate chips per cookie and a standard deviation of 2.1 chocolate chips per cookie

i.e. if X represents the number of chocolate chip cookies, we have X is N(24.1,2.1)

Convert to Z score

`Z = (x-24.1)/(2.1)`

95% upper Z = 1.645 and lower is -1.645

Hence upper p 95 is
`1.645(2.1)+24.1\\= 27.5545`

Lower p 5 would be
`-1.645(2.1)+24.1\\=20.6455`

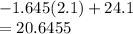
These two values give us an idea that the chocolate cookies should be within these two values.

Answer 2

P5

From Z tables and at P5 = 5% = 0.05, Z = -1.645
Therefore,
True value = mean +Z*SD = 24.1+(-1.645*2.1) = 20.6455 Chips per cookie

P95

From Z table and at P95=95%=0.95, Z= 1.645
Therefore,
True value = 24.1 +(1.645*2.1) = 27.5545 Chips per cookie

These values shows the percentages of amount of chips in the cookies. Thus, the more the percentage considered, the more the amount of chips in the cookies. This can be used to control the number of chips in cookies during production.