Question

the area of a square can be quadrupled by increasing the side length and width by 4 inches. what is the side length?

Answer 1

The number could be anything because whatever it is it can be quadrupled

Answer 2

Let the original side of the square be x inches.When sides are increased by 4 inches the sides are x+4 inches.

Area of square with side x inches=
`x^(2).`

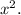
Area of square with sides x+ inches=
`(x+4)^(2).`

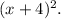
According to question:The area of a square can be quadrupled by increasing the side length and width by 4 inches.\

Or
`4x^(2)=(x+4)^(2)`

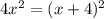
Expanding we have:

`4x^(2)=x^(2)+8x+16.`

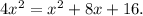
Or,
`3x^(2)-8x-16=0.`

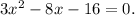
Factoring,

(3x+4)(x-4)=0

3x+4=0 or x=4

x=
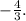`-(4)/(3).` Or x=4.

Sides can not be negative so x=4.

The sides of the square will be 4 inches.