Let the original side of the square be x inches.When sides are increased by 4 inches the sides are x+4 inches.
Area of square with side x inches=

Area of square with sides x+ inches=
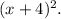
According to question:The area of a square can be quadrupled by increasing the side length and width by 4 inches.\
Or
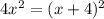
Expanding we have:
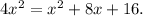
Or,
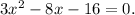
Factoring,
(3x+4)(x-4)=0
3x+4=0 or x=4
x=
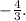 Or x=4.
Or x=4.
Sides can not be negative so x=4.
The sides of the square will be 4 inches.