This problem is mainly concerned with setting up an equation.
let's add the interest rates times their respective investment amounts:
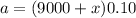
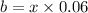
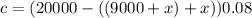
simplify:
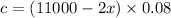
sum of interest:
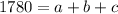
1780 = (9000+x) 0.10 + x 0.06 + (11000-2x)0.08
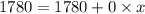
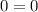
solution:
He does not have any invested in the 6%, while he has 9000 invested at 10% and 11,000 invested at 8%
to check:
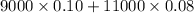
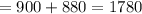
So this ended up being a trick problem because he does not actually have any invested in the 6% option.