Question

A circle has a diameter of 26 units. What is the area of the circle to the nearest hundreth of a square unit?

Answer 1

530.93
The answer for area.

Answer 2

The area of the circle having diameter of 26 is 530.66 square units.

Explanation:

Given:

Diameter of the circle= 26 units

To find:

Area of the circle =?

Solution:

Finding area using Diameter

`\text {Area } A=\pi\left((d)/(2)\right)^(2)`

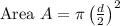
substituting the values we get,

`\text {Area } A=3.14\left((26)/(2)\right)^(2)`

`\text {Area } A=3.14(13)^(2)`

`\text {Area } A=3.14(169)`

`\text {Area } a=530.66 \text { units }`

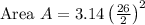
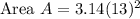
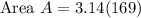
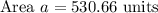
Following methods can also be used to find the area of the circle.

Aliter1: finding area using radius

`\text {radius } r=\frac{\text {diamater}}{2}`

`\text {radius } r=(26)/(2)`

`\text {radius } r=13 \text {units}`

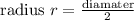
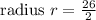
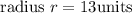
Now ,

`\text {Area } A=\pi r^(2)`

`\text {Area } A=(3.14)(13)^(2)`

`\text {Area } A=(3.14)(169)`

`\text {Area } A=530.66 \text { square units }`

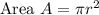
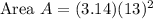
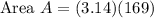
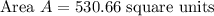
Aliter 2:Finding Area using circumference

Circumference of the circle
`c=2 \pi r`

`c=2 *(3.14)(13)`

`c=2 *(40.82)`

`c=81.64 \text { units }`

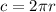
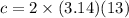
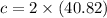
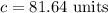
Now

\operatorname
`{Area} A=(c^(2))/(4 \pi)`

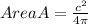
Substituting values,

`\text {Area } A=(81.64)^(2) /(4 \pi)`

`\text {Area } A=(81.64)^(2) /(4)(3.14)`

`\text {Area } A=(665.08) /(4)(3.14)`

`\text { Area } A=(6665.08) /(12.56)`

`\text { Area } A=530.66 \text { square units }`

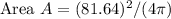
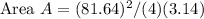
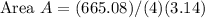
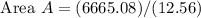
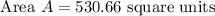
Result:

Thus the area of the circle with a diameter 26 units is 530.66 square units.