Dot product has the following definition:
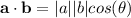
Where
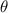
is the angle between two vectors and
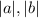
are their lengths.
The dot product of the vector with itself will give you the square of its length.
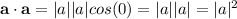
If you are given end points of a vector dot product is defined in the following fashion:
![a=[a_1,a_2,a_3]\\ b=[b_1,b_2,b_3]\\ \textbf{a}\cdot \textbf{b}=\textbf{a} \sum b_i \textbf{e}_i= \sum b_i (\textbf{a} \cdot \textbf{e}_i)= \sum b_i a_i](https://img.qammunity.org/2019/formulas/mathematics/high-school/zs7pn0r35zuqp0ihnz1qgp3b0d0elfeq1x.png)
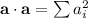
Where
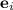
are unit vectors. These are vectors of a unit length and they span in direction of a coordinate axis (if you are working with Cartesian
coordinate system). If you do a dot product of a unit vector of x-axis and unit vector of y-axis you get zero, because the angle between them is 90 degrees.
Now we can apply the above formula to this problem:
![v= [7,24]\\ \textbf{v}\cdot \textbf{v}=|v|^2=(7\cdot 7)+(24\cdot 24)=625\\ |v|=√(625)=25](https://img.qammunity.org/2019/formulas/mathematics/high-school/2e5viwdslr4t0ryg7jx82z4pux9hdr39c3.png)
So the answer is A.
This formula will give you the length of a vector in Euclidian geometry:
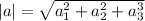
Where
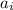 are the coordinates of the end point of that vector.
are the coordinates of the end point of that vector.