Question

Solve the equation by completing the square. Round to the nearest hundredth if necessary. x2 + 3x = 25

Answer 1

we are given

`x^2+3x=25`

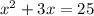
We can complete square

we can write it as

`x^2+2*(3)/(2)*x=25`

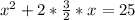
now, we can add both sides (3/2)^2

`x^2+2*(3)/(2)*x+((3)/(2))^2=25+((3)/(2))^2`

now, we can use formula

`a^2+2*a*b+b^2=(a+b)^2`

we can write it as

`(x+(3)/(2))^2=25+((3)/(2))^2`

`(x+(3)/(2))^2=25+(9)/(4)`

`(x+(3)/(2))^2=(109)/(4)`

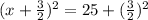
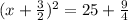
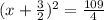
now, we can take sqrt both sides

`\sqrt{(x+(3)/(2))^2}=\sqrt{(109)/(4) }`

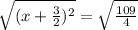
we will get as

first solution:

`x+(3)/(2)=(√(109))/(2)`

`x=-(3)/(2)+(√(109))/(2)`

`x=3.72`

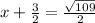
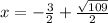
Second solution:

`x+(3)/(2)=-(√(109))/(2)`

`x=-(3)/(2)-(√(109))/(2)`

`x=-6.72`

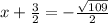
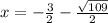
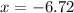
so, solutions are

`x=-6.72`

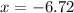
`x=3.72`................Answer