Question

Suppose you have 54 feet of fencing to enclose a rectangular dog pen. The function A = 27x – x2, where x = width, gives you the area of the dog pen in square feet. What width gives you the maximum area? What is the maximum area? Round to the nearest tenth as necessary. width = 13.5 ft; area = 182.3 ft2 width = 13.5 ft; area = 546.8 ft2 width = 27 ft; area = 182.3 ft2 width = 27 ft; area = 391.5 ft2

Answer 1

it will be =182.3 ft^2

Answer 2

The width of the dog pen is 13.5 ft and the area is 182.3 square feet.

Explanation:

We have the function
`A(x) = 27x-x^2` where
`x` is the width of the dog pen. So, if we want to obtain the maximum area, we must find the maximum of the function
`A(x)`.

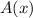In order to accomplish this task, we must calculate the derivative
`A'(x)`:

`A'(x) = 27-2x`.

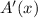The next step is to find the critical points of
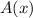`A(x)`, which means to find the values of
`x` where
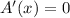`A'(x)=0`. This is equivalent to solve the equation
`27-2x=0`. So,
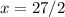`x=27/2`. In order to check if 27/2 is, in fact, a point of maximum we calculate the second derivative

`A'(x) =-2`.

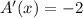Notice that
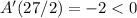`A'(27/2) =-2<0`, and the sufficient condition of the second derivative gives us that
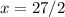`x=27/2` is a maximum.

In order to find the maximal value we evaluate
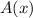`A(x)` at 27/2:

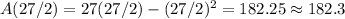`A(27/2) = 27(27/2)-(27/2)^2= 182.25\approx 182.3`.