Answer:
The width of the dog pen is 13.5 ft and the area is 182.3 square feet.
Explanation:
We have the function
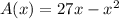 where
where
 is the width of the dog pen. So, if we want to obtain the maximum area, we must find the maximum of the function
is the width of the dog pen. So, if we want to obtain the maximum area, we must find the maximum of the function
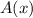 .
.
In order to accomplish this task, we must calculate the derivative
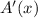 :
:
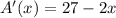 .
.
The next step is to find the critical points of
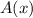 , which means to find the values of
, which means to find the values of
 where
where
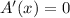 . This is equivalent to solve the equation
. This is equivalent to solve the equation
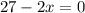 . So,
. So,
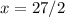 . In order to check if 27/2 is, in fact, a point of maximum we calculate the second derivative
. In order to check if 27/2 is, in fact, a point of maximum we calculate the second derivative
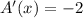 .
.
Notice that
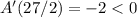 , and the sufficient condition of the second derivative gives us that
, and the sufficient condition of the second derivative gives us that
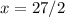 is a maximum.
is a maximum.
In order to find the maximal value we evaluate
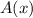 at 27/2:
at 27/2:
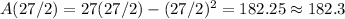 .
.