Question

How many solutions does the equation have, x1 + x2 + x3 = 10 , where x1 , x2, and x3 are non-negative integers?

Answer 1

There are total 66 solutions of the equations.

Explanation:

We can find the solution by fixing the first value i.e.
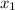`x_1` at a time and shifting the other two values and keep on doing for all the possible values of
`x_1`

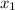
Hence, the possible cases are as follows:

`x_1-x_2-x_3`

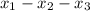
0-10-0 1-9-0 2-8-0 3-0-7 4-0-6 5-0-5 6-0-4

0-0-10 1-0-9 2-0-8 3-7-0 4-6-0 5-5-0 6-4-0

0-1-9 1-1-8 2-1-7 3-1-6 4-1-5 5-1-4 6-1-3

0-9-1 1-8-1 2-7-1 3-6-1 4-5-1 5-4-1 6-3-1

0-2-8 1-2-7 2-3-5 3-2-5 4-2-4 5-2-3 6-2-2

0-8-2 1-7-2 2-4-3 3-5-2 4-4-2 5-3-2

0-3-7 1-3-6 2-3-4 3-3-4 4-3-3

0-7-3 1-6-3 2-2-6 3-4-3

0-4-6 1-4-5 2-6-2

0-6-4 1-5-4

0-5-5

------------------------------------------------------------------------------------------------------------

7-0-3 8-0-2 9-0-1 10-0-0

7-3-0 8-2-0 9-1-0

7-1-2 8-1-1

7-2-1

Answer 2

Non-negative integers are positive integers or zero.

1. When
`x_1=0,` then there are such possible cases for
`x_2` and
`x_3:`

• 
  `x_2=0,\ x_3=10;`
• 
  `x_2=1,\ x_3=9;`
• 
  `x_2=2,\ x_3=8;`
• 
  `x_2=3,\ x_3=7;`
• 
  `x_2=4,\ x_3=6;`
• 
  `x_2=5,\ x_3=5;`
• 
  `x_2=6,\ x_3=4;`
• 
  `x_2=7,\ x_3=3;`
• 
  `x_2=8,\ x_3=2;`
• 
  `x_2=9,\ x_3=1;`
• 
  `x_2=10,\ x_3=0.`

In total 11 solutions for
`x_1=0.`

2. For
`x_1=1,` there are such possible cases for
`x_2` and
`x_3:`

• 
  `x_2=0,\ x_3=9;`
• 
  `x_2=1,\ x_3=8;`
• 
  `x_2=2,\ x_3=7;`
• 
  `x_2=3,\ x_3=6;`
• 
  `x_2=4,\ x_3=5;`
• 
  `x_2=5,\ x_3=4;`
• 
  `x_2=6,\ x_3=3;`
• 
  `x_2=7,\ x_3=2;`
• 
  `x_2=8,\ x_3=1;`
• 
  `x_2=9,\ x_3=0.`

In total 10 solutions for
`x_1=1.`

3. This process gives you

• for
  `x_1=2` - 9 solutions;
• for
  `x_1=3` - 8 solutions;
• for
  `x_1=4` - 7 solutions;
• for
  `x_1=5` - 6 solutions;
• for
  `x_1=6` - 5 solutions;
• for
  `x_1=7` - 4 solutions;
• for
  `x_1=8` - 3 solutions;
• for
  `x_1=9` - 2 solutions;
• for
  `x_1=10` - 1 solution.

4. Add all numbers of solutions:

`11+10+9+8+7+6+5+4+3+2+1=66.`

Answer: there are 66 possible solutions (with non-negative integer variables)