Answer:
There are total 66 solutions of the equations.
Explanation:
We can find the solution by fixing the first value i.e.
 at a time and shifting the other two values and keep on doing for all the possible values of
at a time and shifting the other two values and keep on doing for all the possible values of

Hence, the possible cases are as follows:
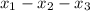
0-10-0 1-9-0 2-8-0 3-0-7 4-0-6 5-0-5 6-0-4
0-0-10 1-0-9 2-0-8 3-7-0 4-6-0 5-5-0 6-4-0
0-1-9 1-1-8 2-1-7 3-1-6 4-1-5 5-1-4 6-1-3
0-9-1 1-8-1 2-7-1 3-6-1 4-5-1 5-4-1 6-3-1
0-2-8 1-2-7 2-3-5 3-2-5 4-2-4 5-2-3 6-2-2
0-8-2 1-7-2 2-4-3 3-5-2 4-4-2 5-3-2
0-3-7 1-3-6 2-3-4 3-3-4 4-3-3
0-7-3 1-6-3 2-2-6 3-4-3
0-4-6 1-4-5 2-6-2
0-6-4 1-5-4
0-5-5
------------------------------------------------------------------------------------------------------------
7-0-3 8-0-2 9-0-1 10-0-0
7-3-0 8-2-0 9-1-0
7-1-2 8-1-1
7-2-1