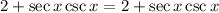Question

"Verify the identity of (sinx cosx)^2/sinx cosx = 2 + secx cscx"

this is for a friend and she's needing help big time

Answer 1

(sinx + cosx)^2/((sinx)(cosx)) = 2 + (secx)(cscx)
(sinx + cosx)^2/((sinx)(cosx)) = 2 + 1/(sinxcosx); subtract 1/sinxcosx both sides
(sinx + cosx)^2/((sinx)(cosx)) - 1/(sinxcosx)= 2; multiply through by sinxcosx
(sinx + cosx)^2 -1 = 2(sinxcosx)
sin^2 + 2sinxcosx + cos^2 - 1 = 2(sinxcosx); since sin^x + cos^2x = 1
1 + 2sinxcosx -1 = 2sinxcosx
2sinxcosx = 2sinxcosx

Answer 2

Step by step answer:

The identity should be:

`\displaystyle ((\sin x+ \cos x)^2)/(\sin x \cos x) = 2 + \sec x\csc x`

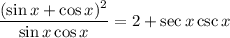
You missed a + there in the numerator, otherwise it would not be an identity.

Expand the square on the numerator:

`\displaystyle (\sin^2x+ 2\sin x\cos x+\cos^2x)/(\sin x \cos x) = 2 + \sec x\csc x`

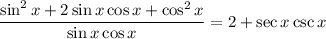
Replace
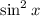`\sin^2x` with
`1-cos^2x\`:

`\displaystyle (1-\cos^2x+ 2\sin x\cos x+\cos^2x)/(\sin x \cos x) = 2 + \sec x\csc x`

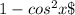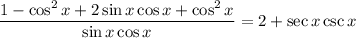
Combine like terms:

`\displaystyle (1+ 2\sin x\cos x)/(\sin x \cos x) = 2 + \sec x\csc x`

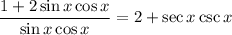
Distribute the denominator through each term of numerator:

`\displaystyle (1)/(\sin x \cos x )+ (2\sin x\cos x)/(\sin x \cos x ) = 2 + \sec x\csc x`

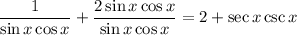
Simplify the second fraction:

`\displaystyle (\sin x)/( \cos x )+ 2 = 2 + \sec x\csc x`

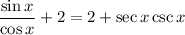
Use the reciprocal identities: sin(x)=1/csc(x) and cos(x) = 1/sec(x):

`\sec x\csc x+ 2 = 2 + \sec x\csc x`

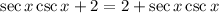
Re-ordering:

`2+\sec x\csc x = 2 + \sec x\csc x`