Question

As the table shows, projections indicate that the percent of adults with diabetes could dramatically increase.

Find A-C.
A. Find a linear model that fits the data in the table, with x=0 for the year 2000.
B. Use the model to predict the percent of adults with diabetes in 2012.
C. In what year does this model predict the percent to be 29.15%?

Answer 1

Bus stage model and make sure you always subtract the monomial

Answer 2

A linear model of the form
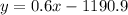`y=0.6 x-1190.9` has been established for predicting diabetes among adults. When applied, this model forecasts a 21.5% prevalence of diabetes among adults in 2012. Furthermore, to reach a prevalence of 29.15%, the calculation from the model indicates a specific future year since 2023, based on the linear equation.

To find a linear model, we need to find the equation of the line that best fits the given data. A linear model has the form:
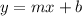`y=m x+b` where:

y is the dependent variable (percent of adults with diabetes),

x is the independent variable (year),

m is the slope of the line, and

b is the y-intercept.

We can use the data for two points to find the slope (m) and y-intercept (b). Let's choose the points (2010, 15.1) and (2020, 21.1):

`\begin{aligned}& m=\frac{\text { Change in } y}{\text { Change in } x}=(21.1-15.1)/(2020-2010) \\& b=\mathrm{y} \text {-intercept }=15.1-m * 2010\end{aligned}`

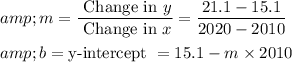
Now, let's calculate m and b:

`\begin{aligned}& m=(21.1-15.1)/(2020-2010)=(6)/(10)=0.6 \\& b=15.1-0.6 * 2010=15.1-1206=-1190.9\end{aligned}`

So, the linear model is
`y=0.6 x-1190.9`

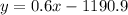
B. To predict the percent of adults with diabetes in 2012 (x=2012), substitute x=2012 into the equation:

`\begin{aligned}& y=0.6 * 2012-1190.9 \\& y \approx 21.5\end{aligned}`

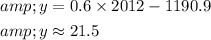
So, the predicted percent in 2012 is approximately 21.5%.

C. To find the year when the model predicts the percent to be 29.15% (y=29.15), substitute y=29.15 into the equation:

`29.15=0.6 x-1190.9`

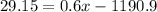
Now, solve for x:

`\begin{aligned}&0.6 x=1219.05\\&x \approx 2031.75\end{aligned}`

So, the model predicts the percent to be 29.15% around the year 2032.