Question

Estimate the error if t6 (trapeziod rule with n=6) was used to calculate ∫30cos(2x)dx.

Answer 1

The error bound for a trapezoid rule is given with this formula:

`|E_t|\leq(K(b-a)^3)/(12n^2)`
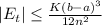
Where n is the number of points we used in the approximation, a and b are starting and ending point of an integral, and K is the number such that:

`|f''(x)|\leq K`
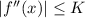
In order to find K we must find the second derivative of our function:

`f(x)=30\cos(2x)\\ f'(x)=-60\sin(2x)\\ f''(x)=-120\cos(2x)`
From this, we can see that our K is 120. This is the amplitude of this periodic function.
Now we can calculate the error bound:

`E_t|\leq(120(b-a)^3)/(12\cdot6^2)=(120)/(432)(a-b)^3`
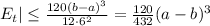
Since you did not specify the interval of integration I cannot compute the final error bound. You can simply plug in the numbers to get the answer.